$600,000
$660,000
9.1%For more information regarding the value of a property, please contact us for a free consultation.
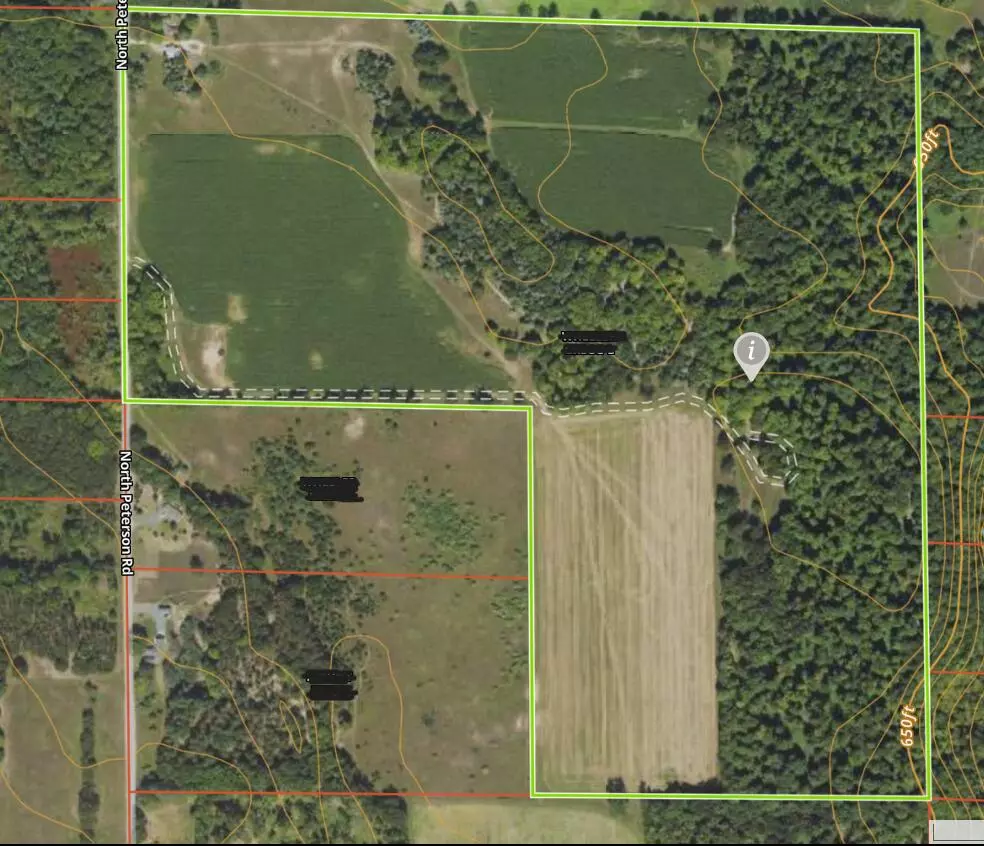
3392 N Peterson Road Ludington, MI 49431
120 Acres Lot
Key Details
Sold Price $600,000
Property Type Vacant Land
Sub Type Acreage
Listing Status Sold
Purchase Type For Sale
Municipality Victory Twp
MLS Listing ID 24021346
Sold Date 05/28/24
Originating Board Michigan Regional Information Center (MichRIC)
Annual Tax Amount $4,500
Tax Year 2024
Lot Size 120.000 Acres
Acres 120.0
Lot Dimensions Irregular
Property Description
Looking for that perfect farm or hunting property? Look no farther than this 120-acre parcel that features 50 acres of tillable land currently in production as well as acres of hardwoods. The topography on the north side of this property is surprising given the level ground in front and provides fantastic wildlife cover and corridors. Hardwoods including maple and cherry fill the northern portion of this parcel and the understory supports deer, bear, turkeys and more. Forester estimate of current maple value is $100,000. This acreage boasts a 1200 SF ranch home that could be revived by the right buyer as well as a handful of storage buildings. There's also a rustic hunting cabin on the property. Also includes 053-015-029-009-00. SHOWN BY APPOINTMENT ONLY. Buyer to verify all information.
Location
State MI
County Mason
Area Masonoceanamanistee - O
Direction From Ludington, take Jebavy Drive North to Decker Road east, which becomes North Peterson Road. Farm is on east side of road about 1.2 miles north of Fisher Road.
Exterior
Utilities Available Phone Available, Electricity Available, Cable Available, Phone Connected, Electricity Connected
View Y/N No
Present Use Hunting,Agricultural
Street Surface Unimproved
Schools
School District Ludington
Others
Tax ID 53-015-029-008-00
Acceptable Financing Cash, Conventional
Listing Terms Cash, Conventional
Read Less
Want to know what your home might be worth? Contact us for a FREE valuation!

Our team is ready to help you sell your home for the highest possible price ASAP

GET MORE INFORMATION